Contenido:
Página de inicio
1. Tablero de dibujo.
2. Neumático de dibujo inercial.
3. Plantillas para líneas discontinuas.
4. Accesorio para construir tangentes y normales a líneas curvas.
5. Cómo dividir una línea y un círculo en partes iguales y desiguales.
Cómo dividir una línea y un círculo en partes iguales y desiguales.
Cómo dividir una línea y un círculo en partes iguales y desiguales. Como regla general, la división de segmentos de línea recta en partes iguales se lleva a cabo de la manera tradicional: mida la longitud del segmento, divida esta longitud por el número de partes y coloque las brújulas en la línea para obtener el tamaño correspondiente varias veces. Dime, ¿a menudo era posible dividir un segmento en pedazos de esta manera la primera vez?
Dividir el círculo en partes iguales (por ejemplo, en la fabricación de bridas, cajas con cubiertas, etc.) también es una tarea que requiere mucho tiempo, especialmente si tiene que dividir el círculo, por ejemplo, entre 7; 8; 9; 10; 11; 13; 14; 15 piezas (Para tal división del círculo no se han desarrollado métodos gráficos).
Por lo tanto, sugiero que los artesanos hagan varios instrumentos simples para resolver de manera rápida, precisa y eficiente los problemas de división de líneas y círculos en partes iguales.
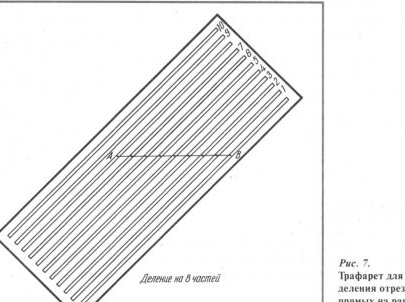
Una de ellas es una plantilla para dividir líneas de plexiglás transparente (Fig. 7). La plantilla tiene ranuras paralelas a través de (ranuras) ubicadas a la misma distancia entre sí. La distancia entre las ranuras generalmente es de 3 ... 50 mm, el número de ranuras es de 3 a 20 ... 50 (para un tamaño de plantilla de 120x250 mm). El ancho de las ranuras es de 0,5 ... 2 mm.
Click para ampliar.
Cuando se trabaja con una plantilla, se coloca en un segmento divisible AB para que un extremo del segmento AB (por ejemplo, el punto A) se alinee con la primera ranura de la plantilla (y en cualquier lugar). El otro extremo del segmento AB (punto B) se combina con la enésima ranura (n es el número de segmentos por los que desea dividir la línea). Tal combinación se puede lograr en solo unos segundos.
Luego, con cualquier elemento de escritura (lápiz, bolígrafo) a través de las ranuras ubicadas entre las ranuras cero y pth, en el segmento AB colocamos marcas de riesgo que dividen el segmento en n partes iguales.La justificación teórica del hecho de que el método propuesto permite dividir cualquier segmento en n partes iguales es el conocido teorema: “Si en un lado de la esquina ponemos algunos segmentos y dibujamos líneas paralelas a través de los puntos obtenidos, se dividen el lado opuesto de la esquina en segmentos proporcionales a (o igual) diferido ".
Pero mas complicado accesorio para resolver el mismo problema, que, por cierto, le permite dividir la línea no solo en partes iguales, sino también en partes que no tienen la misma longitud.
El dispositivo (Fig. 8) consiste en un mecanismo de paralelogramo, que incluye una palanca, tracción conectada a las bisagras, así como uno u otro número de "reglas". La palanca está equipada con controles deslizantes que pueden moverse a lo largo de la palanca y bloquearse en cualquier posición con tornillos especiales. En estos controles deslizantes, con la ayuda de los ejes, se unen "reglas" telescópicas que, a su vez, se conectan mediante bisagras a la tracción. La longitud de las "reglas" telescópicas se puede cambiar a su discreción. Se proporciona una escala de medición en la palanca. En los extremos de las "reglas" telescópicas se montan agujas. Los puntos de fijación de las "reglas" en la tracción dependen de la posición de los controles deslizantes en la palanca. Esto es comprensible, porque de lo contrario el mecanismo de paralelogramo no funcionará.
Click para ampliar.
Suponga que desea dividir el segmento AB en cinco partes iguales. Teniendo tal tarea, el dispositivo se ajusta en consecuencia, es decir, los controles deslizantes se fortalecen a una distancia entre sí igual a la distancia desde el punto A hasta la primera diapositiva. Repetimos, para la instalación de los controles deslizantes hay una escala de medición hecha en la palanca. Por cierto, la distancia del primer control deslizante desde el comienzo de la palanca (punto A) se elige a su discreción. Por supuesto, los "gobernantes" en la tracción también están ajustados a la misma longitud.
Luego, fije el final de la palanca al comienzo del segmento AB (punto A). Luego, actuando por un mecanismo de paralelogramo, además de quitar o empujar (si es necesario) la quinta "regla" telescópica, combine su aguja con el otro extremo del segmento (punto B). Está claro que el resto de la "línea" ocupará una posición paralela a la quinta línea. Después de eso, ajustando la longitud de los "gobernantes" restantes involucrados en la división, coloque sus agujas en el segmento AB. Eso es todo! Dibujado en el segmento, los puntos AB dividirán el segmento en las cinco partes iguales requeridas.
Como ya se mencionó, con la ayuda de este dispositivo es posible dividir el segmento en partes "desiguales" colocando los controles deslizantes en la palanca en las posiciones correspondientes (de modo que las longitudes de los segmentos estén en la proporción correcta).
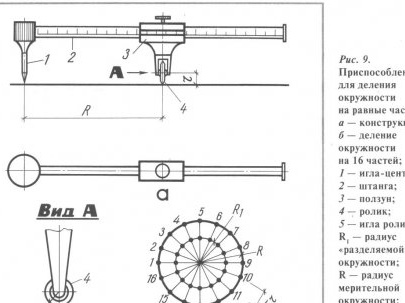
Para dividir los círculos en uno u otro número de segmentos, es adecuado un dispositivo altamente efectivo basado en un calibrador convencional (Fig. 9, a).
Click para ampliar.
En un extremo de la varilla de la pinza (en lugar de la mandíbula fija), se monta una cabeza con una aguja montada. Se monta un disco de medición en el eje del deslizador, en cuyo borde hay una aguja que actúa como elemento de escritura. (El disco puede girar en un plano perpendicular al eje de la barra). Se proporciona una escala en la barra, y la escala se gradúa, de modo que los números impresos indican el número de partes en las que desea dividir el círculo.
Trataremos dicha calibración con más detalle. Suponga que desea dividir un círculo de radio R en 16 partes iguales (Fig. 9.6). Para hacer esto, el puntero del control deslizante se monta en la barra a la marca "16" y el control deslizante se fija con un tornillo. A continuación, colocan la aguja del calibrador a vernier en el centro del círculo, presionan el disco contra el papel y dibujan un círculo completo con brújulas con un radio establecido, que probablemente no será igual al radio Rr. Al correr, la aguja pequeña con la que está equipado el disco dejará 16 marcas en el papel. Ahora, conectando las marcas con el centro del círculo en líneas rectas, obtenemos los riesgos correspondientes en un círculo divisible con un radio, es decir, dividimos el círculo en 16 partes.
¿Cómo funcionó todo? Damos algunos cálculos. Sea r el radio del disco; R, es el radio del círculo divisible; R es el radio del círculo de medición, igual a la distancia desde el control deslizante hasta la aguja (disco) de la brújula; n es el número de partes en que se divide el círculo de medición. Por lo tanto, la longitud de la circunferencia de medición debe ser igual a la circunferencia del disco, multiplicada por el número de divisiones:
2pirn = 2piR o rn = R.
Por lo tanto, para dividir el círculo de medición en n partes, es necesario establecer el control deslizante a una distancia R de la aguja de la brújula, y R será igual a rn. Esta dependencia se usa al graduar la escala. Por ejemplo, prip = 21 ig = 5 mm, el control deslizante debe instalarse a una distancia de R = 105 mm de la aguja. En la escala en este lugar y poner la marca "21".
El dispositivo es de diseño simple, fácil de operar, proporciona una alta precisión de construcción (hasta 0.05 °). La división de cualquier círculo en cualquier número de partes se lleva a cabo en 0.5 ... 2 minutos. Las ventajas del dispositivo son especialmente evidentes cuando se divide el círculo en un número no estándar de segmentos: 5; 7; 9; 11; 13; 14; 15 y otros
Todos los dispositivos de dibujo descritos reducen la complejidad del trabajo de dibujo, eliminan el trabajo de rutina y ayudan a diseñadores, dibujantes, estudiantes, estudiantes en dibujos de dibujo.
Contenido:
Página de inicio
1. Tablero de dibujo.
2. Neumático de dibujo inercial.
3. Plantillas para líneas discontinuas.
4. Accesorio para construir tangentes y normales a líneas curvas.
5. Cómo dividir una línea y un círculo en partes iguales y desiguales.
Cómo dividir una línea y un círculo en partes iguales y desiguales.